20の13乗を18で割った余りを求めよという問題をまじめに解いてみた

飛んできた「18」が「20」をまっぷたつに割る！？

杉もち（@sugimoching）さんの「高校のときの数学小テストでの愚行」と題された画像ツイートが爆発的な人気です。投稿から5日後の2018年8月8日時点で37万を超える「いいね！」。その「愚行」というのは「20¹³を18で割った余りを求めよ」という設問に5コマの漫画で回答したもので、なんと水平になった「18」が猛スピードで飛んできて、「20」を文字通りまっぷたつに「割り」、答えが「13」となるのです。

数学的には正解ではありませんが、人々を感動させる豊かな発想力（そして画力）は充分「加点」に値するものと思います。生き残った「13」のなんともうれしそうな佇まい。ピクサーアニメ並みの展開に拍手喝采です。

さて、すでにオチはついているわけですが、小中と算数小僧だったそらよりはその正解が知りたくてたまらなくなりました。

「20¹³を18で割った余りを求めよ」

無粋とは知りながら、まじめに解いてみました。

アプローチ1．実際に計算して法則を見つける

まず取り組んだのが実際に計算してみることでした。この手の問題には必ず隠れた法則があるはずです。そのパターンを読み解くため「20の1乗」からその余りを割り出してみました。

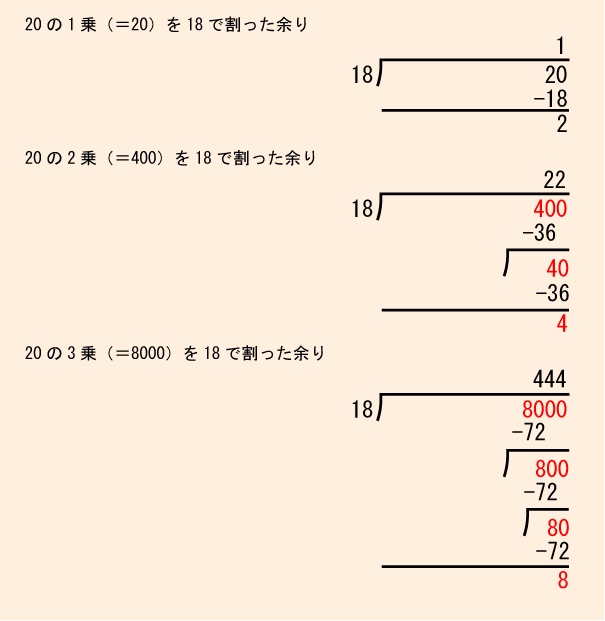
すると狙いどおり、法則めいたものが現れてきました。

乗じて求められた数がそのままひと桁の余り

となっています。

確証を得るためさらに続けてみました。

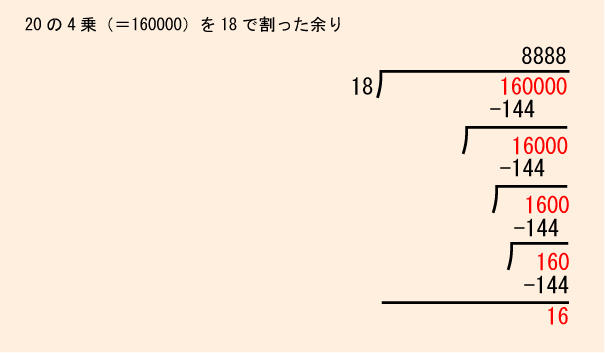
スタートから2倍、2倍、2倍

となっています。

ただし「16」の2倍は「32」。つぎは割る数「18」を超えてしまいます。もしかしたら「32÷18＝1余り14」になったりするのでしょうか。

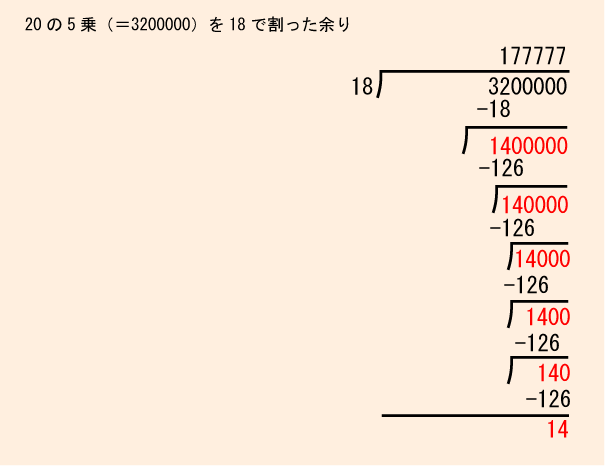
割り算の計算式のスタートはこれまでと異なりますが、答えは予想したとおり「14」になりました。

いえ、スタートは異なりますが、法則は一貫していました。つまり

［20を乗じた答え（今回は「3200000」）から「0」を除いた数「32」＝「2」を同数で乗じた数「32」］を「18」で割った余りが設問の解

です。

上記のように仮定するとつぎは「2の6乗」である「64」を「18」で割った余りである「10」が答えとなるはずです。そして実際に計算してみると「10」となりました。

さらに「2の7乗」である「128」を「18」で割った余りは「2」。おや！　こんどは振り出しに戻りました！

もしかしたら

2→4→8→16→14→10

の順番で循環しているのではないでしょうか。

とすると13番目に巡ってくる数字は？

［1番目］2→［2番目］4→［3番目］8→［4番目］16→［5番目］14→［6番目］10……［12番目］10→［13番目］2となり、今回の設問の正解は「2」であることが予想されます。

念のため検算してみましょう。

「2の13乗」は「『2の6乗』×『2の6乗』×2」です。

つまり「64×64×2」は「8192」。これを「18」で割ると余りは「２」。合っています。よって

答えは２

となります。

アプローチ2．もっとスマートな説明

じつはもっと簡潔に説明できる方法があることにあとで気づきました。

もしかしたら、もっとよい解の導き方があるのかもしれません。ご存知の方は、ぜひコメントをお寄せいただければと思います。